Chapter 7. Knots and Links


	Knots and Links

Chapter 7. Knots and Links

Regina offers native support for knots and links. Regina collectively refers to all such objects as links: a link may have multiple components, or just one component (i.e., a knot), or zero components (i.e., the empty link).

A link is stored using a link diagram, which consists of n crossings and 2n strands that connect them, possibly with some additional unknot components that have no crossings at all.

Regina supports both classical and virtual link diagrams:

Classical link diagrams are the typical planar diagrams that one encounters when first studing knot theory. These describe links in the 3-sphere, and such links are considered to be equivalent under ambient isotopy.
Although classical link diagrams are planar, Regina considers these diagrams to be embedded in the S² (not the plane). In particular, Regina does not keep track of which cell is the “outer” cell of the diagram.
Virtual link diagrams remove the requirement for the diagram to be planar. Instead a virtual link diagram may be embedded in some arbitrary orientable surface S. This describes a link in the thickened surface S × I, and such links are considered to be equivalent under ambient isotopy, orientation-preserving homeomorphisms of S, and the addition and/or removal of empty handles from S.

Links in Regina are oriented. This means that Regina keeps track of a “direction of travel” around each component of the link. Regina also maintains an orientation of the surface containing the link diagram (i.e., S² for a classical diagram, or the orientable surface S for a virtual diagram), which means there is a well-defined notion of left versus right, and positive versus negative crossings.

Creation

The easiest way to create a new link is via the Packet Tree→New Knot or Link menu item (or the corresponding toolbar button).

You will be asked what type of link to create (see the drop-down box below). Here we walk through the various options.

Example Knots and Links

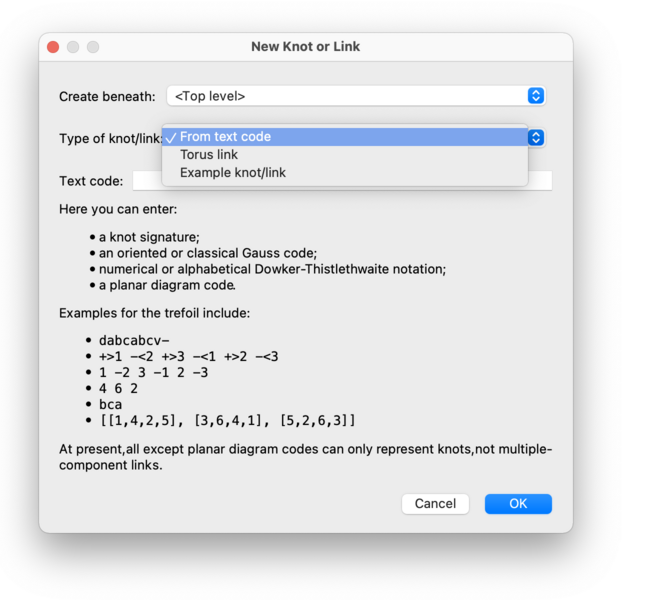
Like triangulations, Regina offers a selection of ready-made sample knots and links which you can use to experiment with Regina. Simply select an example from the list provided and Regina will build the corresponding link for you.

Tip

You can see many more examples by looking through the prime knot census, which is shipped as one of Regina's example data files. Select File→Open Example→Prime Knots from the menu.

Text Codes

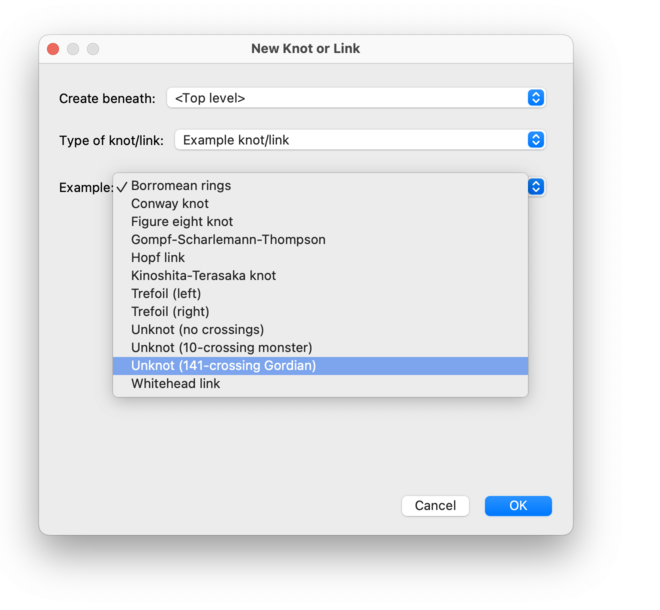
This will reconstruct a link diagram from one of several common text codes.

Be aware: some types of codes only support single-component knots (not multiple-component links), and some types of codes only support classical link diagrams (not virtual link diagrams) – see below for details. If you need all of these features (multiple components and/or virtual diagrams), then good choices are knot/link signatures or planar diagram codes.

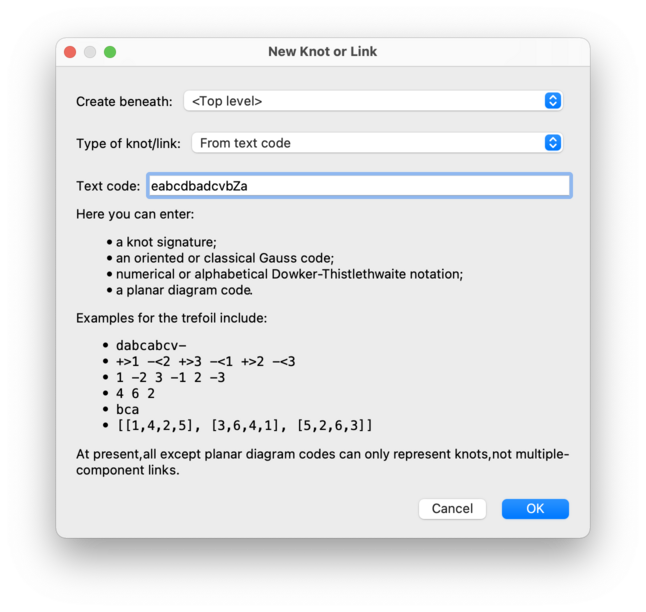
The codes that Regina understands include:

Regina's own knot/link signatures: These are compact sequences of letters, digits and/or punctuation that uniquely identify a link diagram up to combinatorial isomorphism. Here combinatorial isomorphism includes relabelling the crossings and/or components, reflecting the entire diagram, rotating the entire diagram, and/or reversing individual link components.
An example is dabcabcv-, which represents the trefoil.
Knot/link signatures played a significant role in the 19-crossing knot tabulation [Bur20]. They support both classical and virtual link diagrams, and they support all links with fewer than 64 components.
Classical Gauss codes: These are sequences of integers that encode the crossings that you pass through as you traverse the knot from an arbitrary starting point. Crossings are numbered consecutively from 1 to n (but in any order), and each crossing is written as a positive or negative integer according to whether you pass over or under it.
An example of a Gauss code is 1 -2 3 -1 2 -3, which represents the trefoil.
Classical Gauss codes are commonly used in the literature. Be aware that they do not specify the orientation of the diagram, and (more importantly) for composite knots they may not even uniquely define the topology of the knot. If this is a problem, consider using either oriented or signed Gauss codes, or knot/link signatures instead.
In Regina, classical Gauss codes only support knots (not multiple-component links), and they only support classical (not virtual) knot diagrams.
Oriented Gauss codes: These likewise encode the crossings that you pass through as you traverse the knot, but with more precise information than a classical Gauss code. Again the crossings are numbered consecutively from 1 to n (but in any order); each crossing is then written with a sign (+ or -), an arrow (either less-than or greater-than), and a positive integer (which identifies the crossing). The sign indicates whether you pass over (+) or under (-) the crossing, and the arrow indicates whether the other strand of the crossing passes from right-to-left (<) or left-to-right (>).
An example is +>1 -<2 +>3 -<1 +>2 -<3, which represents the left-hand trefoil.
Oriented Gauss codes were introduced by Andreeva et al., and are described as part of their Book Knot Simplifier. Unlike classical Gauss codes, they preserve the orientation of the diagram, and they correctly identify the topology of composite knots.
In Regina, oriented Gauss codes support both classical and virtual diagrams. However, they only support knots (not multiple-component links).
Signed Gauss codes: Like oriented Gauss codes, these encode the crossings that you pass through as you traverse the knot but with more precise information than a classical Gauss code. Once more the crossings are numbered consecutively from 1 to n (but in any order); each crossing is then written with a letter (O or U), a positive integer (which identifies the crossing), and a sign (+ or -). This time the letter indicates whether you pass over (O) or under (U) the crossing, and the sign indicates whether the crossing is positive or negative. There are no spaces in the code at all.
An example is U1+O2+U3-O4-U2+O1+U4-O3-, which represents the figure eight knot.
Oriented Gauss codes were introduced by Kauffman [Kau99]. Like oriented Gauss codes (and unlike classical Gauss codes), they preserve the orientation of the diagram, and they correctly identify the topology of composite knots.
In Regina, signed Gauss codes support both classical and virtual diagrams. However, they only support knots (not multiple-component links).
Dowker-Thistlethwaite notation: This is essentially a more streamlined variant of classical Gauss codes. It has played an important historical role in knot tabulation; see Adams [Ada94] for some history and also a precise description of the format.
Regina understands both the numerical and alphabetical variants of Dowker-Thistlethwaite notation. The numerical variant involves a sequence of n even signed integers. The alphabetical variant transforms this into a compact text string by replacing the positive integers 2,4,6,… with lower-case letters a,b,c,…, and replacing the negative integers -2,-4,-6,… with upper-case letters A,B,C,…. The alphabetical variant can only be used to describe knots with 26 crossings or fewer.
Examples are 4 6 2 or bca, both of which represent the trefoil.
Like classical Gauss codes, Dowker-Thistlethwaite notation does not specify the orientation of the diagram, and (more importantly) for composite knots may not uniquely define the topology of the knot. If this is a problem, consider using either oriented or signed Gauss codes, or knot/link signatures instead.
In Regina, Dowker-Thistlethwaite notation only supports knots (not multiple-component links), and only supports classical (not virtual) knot diagrams.
Planar diagram codes: These are sequences of 4-tuples that encode the local connections around each crossing. Unlike the other code types described here, planar diagram codes can encode multiple-component links.
In a planar diagram code for a link with n crossings, the strands are numbered 1,…,2n. Each 4-tuple represents a single crossing, and lists the four strands that meet at that crossing in counter-clockwise order, beginning with the incoming lower strand. Regina will number the crossings 0,…,(n-1) in the same order as the tuples are presented.
An example of a planar diagram code is [[1,4,2,5], [3,6,4,1], [5,2,6,3]], which represents the left-hand trefoil.
You may separate the integers with any combination of whitespace, commas, round/square/curly brackets, and/or the special symbols PD, X, Xp, Xm or P (these symbols appear in other sources, but have no special meaning for Regina). So, for example, the left-hand trefoil above could instead be presented as PD[X[1,5,2,4], X[3,1,4,6], X[5,3,6,2]], or just 1 5 2 4 3 1 4 6 5 3 6 2.
Planar diagram codes are used in the Knot Atlas (for example). They have two limitations: they cannot represent zero-crossing unknot components; also, if the link has a component that consists entirely of over-crossings (i.e., an unknot placed “on top” of the diagram) then the orientation of that component is not uniquely determined.
In Regina, planar diagram codes support both classical and virtual link diagrams, and they support both knots and multiple-component links.

If you already have a knot or link and you wish to view these different text codes, you can do this through the codes tab.

Caution

Knot/link signatures and Dowker-Thistlethwaite notation are both case sensitive! Be sure that you are entering upper-case and lower-case correctly (or better, copy and paste the text using the clipboard if you can).

Torus Links

Regina can create a new torus link with the given parameters (p, q). This essentially involves drawing a (p, q) curve on an unknotted torus in 3-space and then removing the torus.

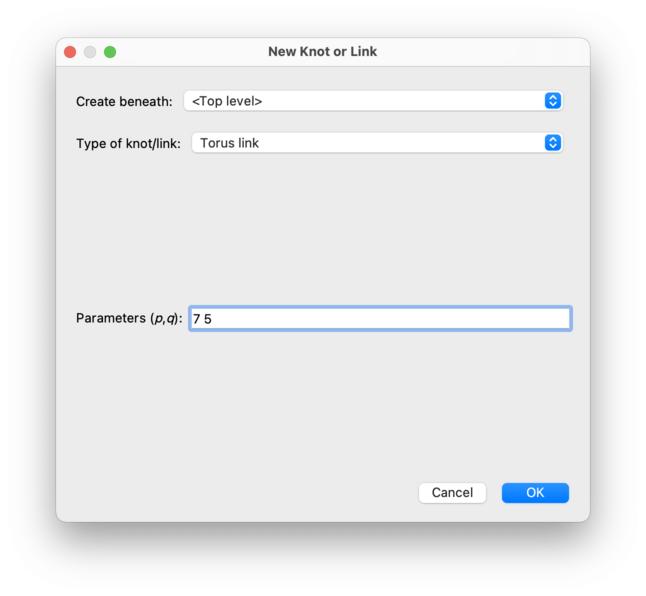
The parameters p and q must be non-negative integers. They do not need to be coprime: if their greatest common divisor is d > 1 then the result will be a link with d components.

Tip

You do not need to separate the lens space parameters with commas; any punctuation, or even just spaces, will suffice.

Whitehead Doubles

Regina can build the Whitehead double of some other knot K. This involves creating two parallel copies of K using the Seifert framing, and then cutting open these two copies and re-connecting them using a clasp. Regina will use positive crossings for the clasp.

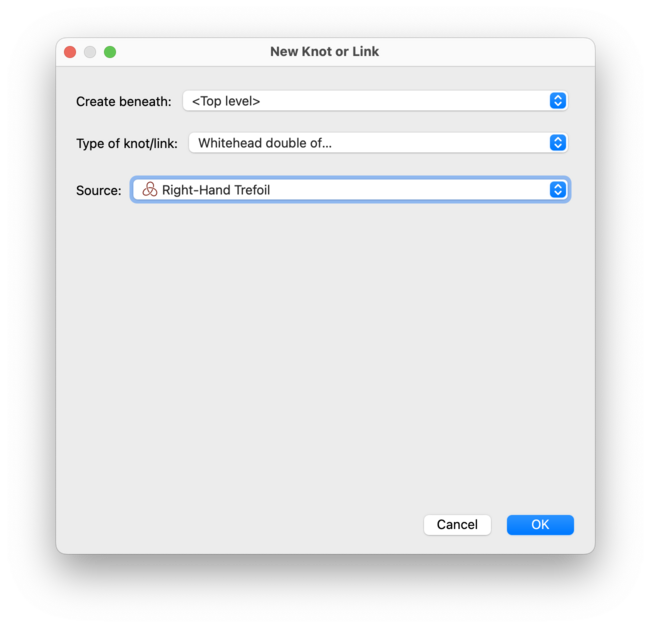
To do this, select K in the Source drop-down box. This should be some knot that you already have in your data file. Note that Regina can only build the Whitehead double of a knot, not a multiple-component link.

Tip

If you already have the source knot K open for viewing, another way to create its Whitehead double is to select Knot / Link→Build Whitehead Double from the menu. The Whitehead double will be added as a new knot directly beneath K in the packet tree.

Parallel Cables

Regina can build a new link containing k cables of some other link L, all parallel to each other via a chosen framing. This will effectively:

treat each component of the original link L as a ribbon, using the chosen framing;
create k parallel copies of L, following each other side-by-side along these ribbons.

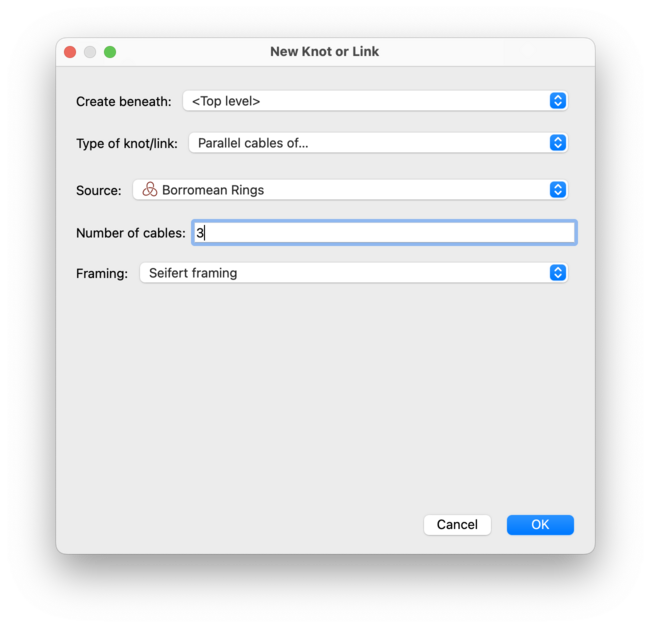
To do this:

Select L in the Source drop-down box. This should be some knot or link that you already have in your data file.
Enter the number of cables k, which should be an integer greater than one (but not too large—see the warning below).
Choose the framing to use. The options are:
Seifert framing
This framing is a property of the underlying link (i.e., it does not depend on your specific choice of link diagram). One way to imagine it is to construct a Seifert surface (an orientable surface embedded in the 3-sphere whose boundary is the link), and then place the ribbons so that they sit flat upon this surface.
Another way to imagine it is purely algebraic: for each component C of the link, each edge of the corresponding ribbon follows a curve with trivial homology in the complement of the knot C.
Blackboard framing
Here each ribbon sits flat in the plane of the link diagram, with no twists. This framing depends on the specific link diagram that you are using.

Warning

The parallel cables construction can generate an enormous number of crossings. If you create k cables then you will multiply the number of crossings in the source link by k², and if you chose the Seifert framing then there may be even more crossings due to twists in the ribbons. Use a large k at your peril!

Tip

If you already have the source link L open for viewing, another way to create parallel cables of L is to select Knot / Link→Build Parallel Cables… from the menu. The parallel cables will be added as a new link directly beneath L in the packet tree.

Prev	Contents	Next
Analysis	Up	Analysis